
DR. A. PETERMANNS
MITTEILUNGEN
AUS
JUSTUS PERTHES' GEOGRAPHISCHER ANSTALT
HERAUSGEGEBEN
VON
PROF. PAUL LANGHANS
56. JAHRGANG
1910
II. HALBBAND

GOTHA: JUSTUS PERTHES
KARTOGRAPHISCHER MONATSBERICHT
| III. Jahrg. |
von Dr. Hermann Haack |
September 1910 |
Die beste bekannte flächentreue
Projektion
der ganzen Erde.
Von Dr. W. Behrmann, Assistent am Geogr. Institut, Berlin.
(Mit
1 Karte, s. Tafel 27.)
Unter der Unzahl der Abbildungsarten, die ins ein Bild der dreidimensionalen Erde auf der zweidimensionalen Ebene geben sollen, gewinnen die flächentreuen Darstellungen immer mehr an Bedeutung. Den energischen Forderungen der Theoretiker muß die Praxis Gehör schenken und sich dazu entschließen, an Stelle der alten, teilweise schlechten Entwurfsarten bessere, neue und besonders flächentreue Projektionen zu setzen. Die aufblühende Wissenschaft der Wirtschaftsgeographie vor allem hat die Wichtigkeit dieser Entwurfsarten erkennen lassen. Doch auch in allen andern Zweigen der Geographie wird man die räumliche Verteilung einer Erscheinung besser beurteilen können, wenn die Räume unmittelbar zum Vergleich geeignet sind, wenn Flächen meßbar, also vergleichbar vor uns liegen. Bei Bildung jeglicher Art von Mittelwerten, sei es z. B. der mittleren Höhe eines Gebietes, der mittleren Regenmenge oder mittleren Bevölkerung, muß man zu flächentreuen Entwürfen greifen. Aber es erübrigt sich wohl, nach den vielfachen Ausführungen in der Literatur 1) den besonderen Wert dieser Darstellungsarten noch einmal hervorzuheben.
Vor allem aber haben die Entwürfe Bedeutung, welche die ganze Erde in einem einheitlichen Gradnetz entwerfen, die es uns ermöglichen, eine Erscheinung über die ganze Erde vergleichbar zu überschauen. Und so hat sich der Kampf für die flächentreuen und gegen die vermittelnden und winkeltreuen Projektionen gerade gegen die Mercatorprojektion gerichtet, weil ja diese Darstellungsart vor allen zur Abbildung der ganzen Erde, man kann sagen noch bis auf den heutigen Tag, nur zu häufig benutzt wird. Der Grund dafür ist ein sehr praktischer. Die Zeichnung des geradlinigen Netzes ist bei der Mercatorkarte sehr leicht. Die waagrechten Parallelkreise ermöglichen eine leichte Übersicht der geographischen Breiten, wie die senkrechten Meridiane die der Längen. Klima und Zeit sind dadurch in ihren Hauptgrundzügen übersichtlich geboten. Jeder Ort läßt sich durch rechtwinklige Koordinaten leicht eintragen. Die Praxis der Nautik kann auf diese Karten nicht verzichten. Die Projektion ist winkeltreu und hat den großen Vorzug, der einzige Entwurf dieser Art zu sein (die stereographische Projektion mit ihrem Darstellungsgebiet über die ganze unendliche Ebene kommt nicht in Frage), die es ermöglicht, die Erde, wenn auch nicht ganz, so doch bis zu. den nördlichsten Gebieten darzustellen. Man ist also der Auswahl überhoben, kann sich Umrißkarten dieser einzigen Projektion in verschiedenen Maßstäben entwerfen und so billige Karten durch Überdrucke herstellen.
Wollen wir also erfolgreich den Kampf gegen die allein seligmachende Mercatorkarte aufnehmen, so müssen wir eine Projektion vorschlagen, die die Vorteile der Mercatorkarte mit den Vorteilen einer flächentreuen Projektion verbindet. Natürlich wird unsere Karte nicht winkeltreu sein, dafür aber die ungeheuren Flächenverzerrungen vermeiden, sie wird als äquivalente Karte die Darstellung der Erde in einem geschlossenen Raum ermöglichen, ohne daß ein Teil in die Unendlichkeit rückt. Ein flächentreuer Entwurf, der geeignet wäre, in der Praxis die Mercatorkarte wirklich zu verdrängen, müßte also vor allem zwei Forderungen erfüllen : erstens muß er der beste flächentreue Entwurf sein, damit er als einziger der Mercatorkarte gegenübergestellt werden kann und so die gleichen für die Praxis wichtigen Erleichterungen verschafft wie dieser; zweitens muß er ebenso leicht herzustellen sein und ebenso übersichtliche Beziehungen zwischen Länge und Breite bieten wie Mercator 2).
Wir hätten also zuerst zu fragen, welche flächentreue Projektion der ganzen Erde theoretisch von den bekannten die, beste ist, um dann zu untersuchen, ob sie in der Praxis den eben erhobenen Forderungen genügt.
Gerade in neuerer Zeit ist eine Anzahl von flächentreuen Projektionen vorgeschlagen, die häufig nur dadurch entstehen, daß aus einer Reihe schon bekannter Variationsmöglichkeiten ein Spezialfall als besonders geeignet herausgegriffen wird. Aber keine von allen überragt die andern weit, ja es dürfte heute selbst dem Kenner schwer sein, ohne mathematische Untersuchungen einer der empfohlenen Entwurfsarten entschieden den Vorrang zu geben. So ist durch die neuen Vorschläge keine Vereinfachung, sondern eher eine Verwirrung entstanden. Es scheint mir daher der Wert der Untersuchung auch darin zu liegen, daß sie das Ersinnen von Projektionen erschwert. Denn künftighin wird man verlangen müssen, daß von jeder neu vorgeschlagenen Darstellungsweise der oft nicht leicht zu führende Beweis geliefert ist, (daß sie die beste bisher bekannte Projektion überragt. So soll die Untersuchung eine Anzahl von Entwurfsarten auszumerzen helfen. Denn es dürfte unsere Aufgabe sein, die Zahl der Projektionen zu vermindern, nicht zu vermehren.
Kann man über die flächentreuen Projektionen ein unumstößliches Werturteil fällen? Nach, den Untersuchungen Tissots 3) muß man diejenige flächentreue Projektion als die beste ansprechen, die die geringsten Winkelverzerrungen aufweist. Bei allen Entwürfen dieser Art hängt nämlich die Zunahme der Längenverzerrungen unmittelbar ab von den Verzerrungen der Winkel. Natürlich werden wir nicht die Projektion als die beste bezeichnen, die zufällig einen geringen extremen Wert der Verzerrungen aufweist neben sonst hohen Beträgen, sondern werden uns nach dem Mittelwert der Verzerrungen auf dem ganzen darzustellenden Gebiet, in unserem Falle der ganzen Erde, richten müssen. Diese Erkenntnis hat vornehmlich die Debatte über die beste Karte des afrikanischen Kontinents erbracht 4). In jedem Punkt der Karte bestimmen wir aber nur den Maximalwert der auftretenden Verzerrung 2w, von diesem hängen auch die Längenverzerrungen ab. Es wird in jedem Punkt je nach der gewählten Richtung jeder Verzerrungswert von 0 bis zu diesem Maximalwert beliebig oft erreicht, ohne daß sich ein Mittelwert an diesem Punkt bilden ließe. Wir werden daher als Kriterium für die Güte der Projektion die mittlere Maximalwinkelverzerrung setzen müssen. Es sei nur von Anfang an darauf aufmerksam gemacht, daß, wie jeder Mittelwert von der Umrandung des Gebietes abhängt, so auch der unsrige. Es ist also die beste Projektion der Erdkugel keineswegs die beste für ein Teilstück derselben.
Die Bestimmung der mittleren Maximalwinkelverzerrung kann ebenso unternommen werden wie z. B. die Bestimmung der mittleren Regenhöhe eines Gebietes. Man muß sich zuerst für die zu untersuchende Karte die Linien gleicher maximaler Winkelverzerrung zeichnen. Die flächentreue Entwurfsart erlaubt sofort ein Planimetrieren der von einer dieser Kurven umschlossenen Fläche. Dann konstruiert man ein Diagramm, in dem man waagrecht die so gefundenen Flächenräume und senkrecht die dazugehörigen Verzerrungen durch proportionale Teile aufträgt. Die mittlere Höhe dieses Diagramms ergibt die gesuchte mittlere Maximalwinkelverzerrung.
Die Schwierigkeit der Aufgabe liegt, wie man sieht, nur in der Zeichnung der Äquideformaten. Nur für die wenigsten Projektionen sind dies mathematisch leicht zu definierende Kurven. Nachdem aber von Tissot das Verzerrungsgesetz für den allgemeinsten Fall einer Kartenprojektion aufgestellt ist, handelt es sich nur noch um Anwendungen dieser Formel. Für eine große Anzahl von Entwurfsarten hat Tissot selbst Verzerrungselemente berechnet. Es bleibt also nur noch die Aufgabe zu lösen übrig, die Berechnungen so weit auszudehnen, daß eine Zeichnung der Kurven gleicher maximaler Winkelverzerrung möglich ist, bzw. für die noch fehlenden Projektionen die Anwendung der Tissotschen Formel zu bieten.
Dieser Aufgabe habe ich mich in einer soeben erschienenen Arbeit 5) unterzogen; sie gibt die mathematischen Entwicklungen sowie die Tabellen zur Zeichnung der Äquideformaten. Die so erhaltenen Kurven geben interessante Bilder. Doch kann es nicht meine Aufgabe sein, hier die Ausführungen zu wiederholen. Es sei nur kurz das Resultat mitgeteilt, um dann auf die Besprechung der besten Projektion einzugehen.
Es ergab sich als mittlere
Maximalwinkelverzerrung für die flächentreue Darstellung der ganzen Erde in 2wd:
|
|
||||||||||||||||||||||||||||||||||||||||
Die Zusammenstellung dürfte die bekannten, in Frage kommenden flächentreuen Projektionen der Erde erschöpfen. Flächentreue Kegelprojektionen kommen für die Darstellung der ganzen Erde nicht in Frage, also auch nicht ihre "unechten" Abwandlungen. Höchstens Stab-Werners Projektion kann auf die Erde ausgedehnt werden, doch kann diese ernstlich nicht mit den andern Projektionen konkurrieren.
Es ergibt sich ans der Tabelle das Resultat, daß nach den Forderungen der Theorie die beste bisher bekannte flächentreue Projektion der ganzen Erde, also die Projektion, die Flächentreue verbindet mit der geringsten mittleren Winkelverzerrung und somit auch mit der geringsten mittleren Längenverzerrung, die flächentreue Projektion auf den Durchschnitts-Zylinder im 30. Parallelkreis ist. Dieser Projektion steht die Eckertsche Projektion 6) mit Ellipsen als Meridianen nur wenig nach.
Es erhebt sich also jetzt die Frage, ist diese theoretisch beste Projektion für die Praxis zu empfehlen oder ergeben sich bei der Darstellung der Erde in dieser Form häßliche und störende Verzeichnungen. Denn ganz ohne diese kann keine Projektion auskommen, sie müssen nur in Gebiete von nicht zu großer kultureller Bedeutung verschoben werden, außerdem muß sowohl die Umrandung des Bildes wie die gegenseitigen Lagenverhältnisse ein erfreuliches Aussehen haben.
Entwerfen wir uns eine Karte 7) in dieser Projektion, so wird man im allgemeinen das Erdbild als ein gutes zu bezeichnen haben. Entsprechend der Zunahme der Winkelverzerrungen zum Äquator sehen wir zwar Afrika, die ostindische Inselwelt und den Norden von Südamerika etwas in die Länge gezogen, doch ist der Betrag nur so gering, daß man ihn gern in den Kauf nehmen wird.
Überhaupt ist das Bild der Erde innerhalb der Parallelkreise 48° 21' N und S ein sehr befriedigendes, d. h. es lassen sich nicht weniger als 381 Mill. qkm, oder etwa drei Viertel der Erde, in einwandfreier Weise darstellen. Mäßige Verzerrungen finden wir zwischen dem Parallelkreis 48° 21' und 60°, also auf einem Flächenraum von 60,6 Mill. qkm, große Verzerrungen zwischen 60° und 68° 56', also für 34,2 Mill. qkm, endlich unbrauchbar sind die Polarkalotten vom Parallelkreis 68° 56' an oder 34,1 Mill. qkm. Dieselben Zahlen würden für die Eckertsche Ellipsenprojektion betragen 367,5; 96,7; 34,4; 11,3 Mill. qkm. Wir sehen also, daß für diese Projektion die guten Partien (Verzerrungen zwischen 0° und 30°) kleiner, die mäßig guten (zwischen 30° und 60°) dagegen etwas größer ausfallen, u m endlich für ein etwas kleineres Stück der Erde überhaupt unbrauchbar (Verzerrungen über 90°) zu sein. Es ist also auch diese Projektion nicht wesentlich schlechter als die erstgenannte. Und doch möchte ich der Zylinderprojektion mit längentreuem 30. Parallelkreis bei weitem den Vorrang geben. Eckert rühmt an seinen Projektionen einen Vorzug, den er auch dem Mollweideschen Entwurf zugesteht, daß die Parallelkreise wirkliche parallele Geraden geworden sind, man also ohne Schwierigkeit den Blick von 0 nach W schweifen lassen kann, um eine Anschauung der Lagenverhältnisse zu erhalten, ferner, daß man bei geraden Parallelkreisen leichter Namen eintragen kann. Denselben Vorteil aber hat auch die Zylinderprojektion. Zu diesem tritt der zweite, daß die Lagenverhältnisse in der Richtung der Meridiane in gleicher Weise leicht übersichtlich sind. Wir orientieren uns auf der Erde nun einmal nach Länge und Breite; diese Beziehungen also in möglichst einfacher Form zu bieten, muß daher immer mit Vorteil verbunden sein. Man vergleiche nur die Lage Japans zu Australien oder San Franziskos zu Kap Horn auf unserer Karte und man wird den Vorteil der neuen Projektion gegenüber Eckerts und besonders Mollweides Projektion augenfällig erkennen.
Der Hauptnachteil der Projektion besteht darin, daß man die Konvergenz der Meridiane zum Pol nicht erkennt, daß also die Gebiete in nördlichen und südlichen Breiten weit auseinandergezogen sind. Auch kann man sich schwerer als bei Eckert eine Vorstellung davon machen, daß das gebotene Bild die Darstellung einer Kugel sein soll. Doch, glaube ich, ist dieser Nachteil gleichzeitig mit einem großen Vorteil verbunden. Da die Meridiane alle als parallele gleichabständige Geraden erscheinen, so ist kein Meridian vor dem andern bevorzugt, das Bild mit denn Nullmeridian als Mitte unterscheidet sich in nichts von dem mit einem andern Meridian als Mittellinie. Aus diesem Umstand ergibt sich der weitere Vorteil, daß man die Erdräume, die durch den Randmeridian künstlich seziert werden, an der andern Seite der Projektion wiederholen kann. Bei keiner andern flächentreuen Projektion kann man von diesem Umstand Gebrauch machen, der bei der Mercatorprojektion schon oft mit großem Nutzen angewandt ist. Gegen den Einwurf, man dürfe keine Projektion vorschlagen, bei der unendliche Längenverzerrungen, wie bei uns am Pol, vorkommen, sei erwidert, daß in diesem Falle nur die von Collignon, Hammer oder Sanson-Flamsteed in Frage kämen, also alles Projektionen mit großer mittlerer Maximalverzerrung. Denn auch Mollweide hat am Pol eine Verzerrung von 180°, also unendliche Längenverzerrungen. Diese drei Projektionen stellen aber alle Punkte des Randmeridians zweideutig dar, während bei der Zylinderprojektion nur der Pol vieldeutig geboten wird. Es läßt sich eben keine zweidimensionale Projektion angeben, bei der Eindeutigkeit gewahrt bleibt ohne unendliche Verzerrungen zu besitzen.
Nach allein erscheint mir die Projektion auf dem Durchschnittszylinder im 30. Parallelkreis nicht nur in bezug auf den Mittelwert der Verzerrungen die Eckertsche Projektion zu übertreffen, sondern auch in der überaus bequemen Art der Konstruktion und den dadurch bedingten Lagenverhältnissen. Doch auch die Lage der Flächen ohne Verzerrung scheint mir günstiger zu sein. Bei Eckert (ähnlich bei Mollweide) erscheinen nur zwei Punkte ohne Verzerrung, die auf dem Mittelmeridian der Darstellung etwas nördlicher bzw. südlicher als 40° liegen. Dadurch wird der künstlich heraus gegriffene Meridian noch mehr begünstigt. Der Äquator hat die Verzerrung von 19° 16'. Bei der Zylinderprojektion dagegen erscheinen beide Parallelkreise 30° ohne Verzerrungen, der Äquator weist nur eine Verzerrung von 16° 25' auf. Die günstigen Zonen legen sich also gleichmäßig um die ganze Erde, es werden nicht zwei Punkte willkürlich herausgegriffen. Die Zone um den 30. Parallelkreis trifft Gebiete, die auf der nördlichen Halbkugel in China und Amerika mit großen Kulturregionen zusammenfallen, in Europa und Afrika verläuft sie allerdings etwas südlich der wichtigsten Gebiete, auf der südlichen Halbkugel werden gerade die Hauptkulturgebiete berührt. Doch wird auch in Europa, das leider wegen seiner nördlichen Lage sich schlechter darstellt, die Verzerrung von 40° erst bei 52° 40' erreicht, also in Breiten von Berlin-Liverpool, die Verzerrung von 50° erst bei 56° 31', also in Breiten von Riga – Kattegat - Dundee; die Verzerrung von 60°, die wohl als Grenze der mäßigen Verzerrungen anzusehen ist, trifft St. Petersburg - Christiania. Die Polarregionen, die doch entschieden wertlosesten der Erde, erscheinen am verzerrtesten.
Es scheint mir also diese Projektion nach allem nicht nur theoretisch, sondern auch praktisch die beste aller bekannten flächentreuen Projektionen zu sein. Sollte es sich einbürgern, die Erde in dieser Form abzubilden, so glaube ich, wird die Projektion ein großes Gegengewicht gegen die falschen Vorstellungen bilden, die durch die Mercatorkarte hervorgerufen sind. Da beide Projektionen aus den gleichen geraden Linienelementen zusammengesetzt sind, so ist ein Vergleich beider Karten leicht. Die eine Karte wird die Fehler der andern unschwer erkennen lassen. Die Mercatorkarte aber ist für einzelne Wissensgebiete unentbehrlich, die Gegenüberstellung einer leicht vergleichbaren Karte ist also aus pädagogischem Interesse wertvoll.
Sollte man aber trotz allem eine Krümmung der Meridiane für unerläßlich halten, so werde die Eckertsche Ellipsenprojektion angewandt; glaubt man endlich die Meridiane in einem Punkt zusammenlaufen lassen zu müssen, so ist Mollweides Projektion für die Darstellung der ganzen Erde zu wählen 8).
Um aber der nach obigem besten Projektion der ganzen Erde in flächentreuer Darstellungsweise Eingang zu verschaffen, sei auf der beigefügten Karte die Erde auf den Durchschnittszylinder im 30. Parallelkreis dargestellt. Der Maßstab der Karte 1:100 Mill. bezieht sich auf die ganze Fläche oder auf den 30. Parallelkreis, die Maßstabänderung für die andern Parallelkreise und für die Meridiane mit den wachsenden Breiten ist aus den seitlichen Diagrammen zu erkennen. Endlich sei in einer Tabelle die Länge der Parallelkreise und ihr Abstand vom Äquator (ohne Berücksichtigung der Erdabplattung) geboten, um eine schnelle Zeichnung der Karte zu ermöglichen.
| Länge der Parallelkreise 2Rp*cos 30° = 34 663 km | |||
| Länge der Meridiane 2R / cos 30° = 14 771,6 km | |||
| Abstand der Parallelkreise vom Äquator R sin j / cos 30° | |||
| j | h | j | h |
| 0° | 0,0 km | 50° | 5634,9 km |
| 5° | 641,1 km | 55° | 6025,5 km |
| 10° | 1277,3 km | 60° | 6370,3 km |
| 15° | 1903,8 km | 65° | 6666,6 km |
| 20° | 2515,8 km | 70° | 6912,2 km |
| 25° | 3108,7 km | 75° | 7105,1 km |
| 30° | 3677,9 km | 80° | 7244,0 km |
| 35° | 4219,1 km | 85° | 7327,8 km |
| 40° | 4728,2 km | 90° | 7355,8 km |
| 45° | 5201,3 km | ||
Tafel 27
Anmerkung: Nachfolgende Karte wurde neu projiziert und stimmt NICHT mit dem Original überein.
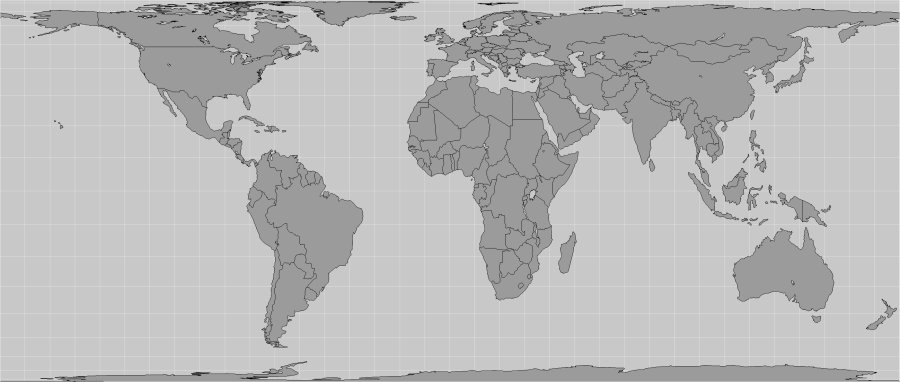
Flächentreue
Projektion auf den Durchschnitts-Zylinder im 30. Grad
(die beste bekannte flächentreue Projektion der ganzen Erde)
Mittlere Maximalverzerrung 2 wd = 27° 6'
1) K.
Peucker : Drei Thesen zum Ausbau der theoretischen Kartographie. (G. Z.
VIII, 1902, S. 66.)
Petermanns Geogr. Mitteilungen. 1910, II, Heft 3.
2) H.
Haack schreibt über die Wichtigkeit einer praktischen Projektion im G.
Jb. 1906, S. 348: "Selbst wenn ein Entwurf ausgedacht würde, der
unstreitig nach der wissenschaftlichen als auch nach der praktischen Richtung
hin - die Bedeutung dieser darf im vorliegenden Fall keineswegs unterschätzt
werden - vor Mercator den Vorzug verdiente, so dürfte man sich seinen Siegeszug
durch die Atlanten keineswegs als einen Sturmeslauf vorstellen: Tausende von
wertvollen Platten wirft man nicht gern einem Kartennetz zuliebe zum alten
Eisen."
3)
M. A. Tissot: Memoire sur la
representation des surfaces et des projections des cartes geographiques. Paris
1881.- Deutsche Bearbeitung von E. Hammer:
Die Netzentwürfe geographischer Karten nebst Aufgaben über Abbildung-
beliebiger Flächen aufeinander. Stuttgart 1887.
4)
Vgl. die Arbeiten von
Zöppritz, Hammer
und Bludau in der Z. d. Ges. f. E. XIX, XXIV, XXVI, XXVII und in Pet.
Mitt. 1892.
5)
W.
Behrmann: Zur Kritik der flächentreuen Projektionen der ganzen Erde und
einer Halbkugel. (Sitzb. der Kgl. Bayr. Ak., math.phvs. Kl., München 1909, 13.
Abh.)
6) M.
Eckert: Neue Netzentwürfe für Erdkarten. (Pet. Mitt. 1906, S. 97 mit
K.)
7) S. Taf. 27.
8) Hammers
Satz: "Für flächentreue Darstellungen der ganzen Erdoberfläche halte ich
die Hammersche Abbildung im allgemeinen für besser als die Mollweidesche,
besonders wenn es auf Darstellungen um den Mittelpunkt ankommt", wird man
wohl seine Zustimmung verweigern müssen. Zwar ist Hammers Projektion im
Mittelpunkt winkeltreu, Mollweides dagegen nur für zwei Punkte des
Mittelmeridians in etwa 42° N und S, während der Äquator Verzerrungen von 12°
1' aufweist, doch übertrifft Mollweide mit einer mittleren
Maximalwinkelverzerrung von 32° 7' Hammer mit 37° 34' so bedeutend, daß man
dieser Darstellung den Vorrang geben wird, zumal die Konstruktion leichter ist
und das Kartenbild parallele Geraden als Parallelkreise zeigt.
Von: "Jürgen HEYN" <j.heyn@gmx.de>
An: <perthes@klett-mail.de>
Betreff: Bitte um Genehmigung
Datum: Freitag, 14. Februar 2003 09:35
Jürgen Heyn
Justus Perthes Verlag Gotha GmbH
Justus-Perthes-Str. 3-5
99867 Gotha
Telefon: 03621/385-0
E-Mail: perthes@klett-mail.de
Sehr geehrte Damen und Herren,
vor einigen Wochen waren Sie so freundlich, mir eine Fotokopie eines Beitrages aus "Petermanns geographischen Nachrichten" zu schicken.
Es handelte sich um den Aufsatz von Dr. Walter Behrmann "Die beste bekannte flächentreue Projektion der ganzen Erde", erschienen 1910.
Ich habe diesen Aufsatz digitalisiert und würde ihn gerne auf meiner Internetseite als Referenz anbieten. Auszüge aus dieser Publikation sind selbst bei angesehenen Bibliotheken nicht oder nur unter erschwerten Bedingungen zu erhalten. Es wäre sehr nett, wenn Sie mir die Veröffentlichung genehmigen würden. In der Anlage finden sie die entsprechende Datei (im *.html Format).
Bei meiner Internetpräsentation www.heliheyn.de handelt es sich um eine private Seite ohne jegliche kommerzielle Absichten.
Wenn Sie es wünschen würde ich der Datei selbstverständlich einen Hinweis anfügen; ähnlich: "Mit freundlicher Genehmigung ...
Des weiteren könnte ich einen Link (Verweis) auf eine Ihrer Seiten damit verbinden.
Im Voraus vielen Dank für Ihre Mühe.
Mit freundlichen Grüssen
Jürgen Heyn
PS: Nochmals vielen Dank für die kostenlosen Kopien. Ist es generell möglich über Sie Kopien von Aufsätzen aus den "Petermanns Geographischen Nachrichten" zu erhalten? Selbstverständlich dann gegen Erstattung von Unkosten und Porto.
Von: "Juliane Pinnau" <j.pinnau@klett-mail.de>
An: "'Jürgen HEYN'" <j.heyn@gmx.de>
Betreff: AW: Bitte um Genehmigung
Datum: Freitag, 14. Februar 2003 11:24
Sehr geehrter Herr Heyn,
Sie können den Aufsatz aus PGM gerne auf Ihre Homepage stellen. Wir bitten
um Ihr Verständnis, dass wir selbst gegen Kostenerstattung keine weiteren
Aufsätze für Sie kopieren können.
Mit freundlichen Grüßen
KLETT-PERTHES
Juliane Pinnau