| Select english language |
Wie funktioniert die Peters-Konstruktion ?
1. Die Gestalt der Erde
2. Die Einteilung der Erdoberfläche
3. Besonderheit des Breitenkreises
4. Nur ein bisschen Mathematik
5. Die Vision von Arno Peters
6. Landkarten durch Projektion
7. Das Netzmaschensystem
8. Koordinaten einzeichnen
9. Die Dezimalkarte
Vorwort
In den mir vorliegenden Veröffentlichungen wird die
Peters-Konstruktion beschrieben. Leider, wie so oft in der Fachliteratur, für den
interessierten Laien schwer verständlich.
Ich habe versucht, die erforderlichen Vorkenntnisse und den Ablauf der Konstruktion
allgemein verständlich zu beschreiben.
Mit der Erkenntnis, dass die Erde keine Scheibe sondern kugelförmig sein muss, ist im Verständnis des Weltbildes ein entscheidender Wandel eingetreten.
 |
 |
Schneidet man eine Kugel durch deren Mittelpunkt, so ergibt die Schnittfläche immer einen Kreis. Der Kreis ist eine geometrische Figur deren mathematische Berechnung mit der Kreiszahl p = 4*arctan(1) = 3,14... recht einfach ist.
Leider ist die Erde aber keine Kugel. Schneidet man die Erde durch Nord- und Südpol so ist die Schnittfläche eine Ellipse. Dieser Umstand ist ärgerlich, weil eine Ellipse mathematisch wesentlich komplizierter zu berechnen ist. Im Gegensatz zu einem Kreis besitzt eine Ellipse zwei Radien. Die große Halbachse a und die kleine Halbachse b.

Die Erde dreht sich relativ gleichförmig um die Polachse. Das heißt jeder Punkt auf
der Erdoberfläche beschreibt innerhalb eines Tages eine kreisförmige Bahn um die
Polachse. Demzufolge ist die Schnittfläche durch den Äquator ein Kreis. Daraus
resultiert, das die Erde ein - wenn auch nur geringfügig - abgeplattetes
Rotationsellipsoid ist.
Im Laufe der Jahre wurden unzählige sogenannte Referenzellipsoide vermessen. Die
Abplattung f wird nach folgender Formel errechnet:
f = (a - b ) / a
"e" ist das Maß für die Abweichung einer Ellipse von der Kreisform und wird numerische Exzentrizität genannt. Je kleiner e ist, desto "kreisähnlicher" ist die Ellipse.
Ellipsoid |
große Halbachse a (m) |
kleine Halbachse b (m) |
Abplattung f |
1 / f |
e |
Airy 1830 |
6377563,396 |
6356256,909 |
0,003340850641 |
299,324964600 |
0,0816733739 |
Modified Airy |
6377340,189 |
6356034,448 |
0,003340850641 |
299,324964600 |
0,0816733739 |
Australian National |
6378160,000 |
6356774,719 |
0,003352891869 |
298,250000000 |
0,0818201800 |
Bessel 1841 (Namibia) |
6377483,865 |
6356165,383 |
0,003342773182 |
299,152812800 |
0,0816968312 |
Bessel 1841 |
6377397,155 |
6356078,963 |
0,003342773182 |
299,152812800 |
0,0816968312 |
Clarke 1866 |
6378206,400 |
6356583,800 |
0,003390075304 |
294,978698200 |
0,0822718542 |
Clarke 1880 |
6378249,145 |
6356514,870 |
0,003407561379 |
293,465000000 |
0,0824834000 |
Everest (India 1830) |
6377276,345 |
6356075,413 |
0,003324449297 |
300,801700000 |
0,0814729810 |
Everest (Sabah Sarawak) |
6377298,556 |
6356097,550 |
0,003324449297 |
300,801700000 |
0,0814729810 |
Everest (India 1956) |
6377301,243 |
6356100,228 |
0,003324449297 |
300,801700000 |
0,0814729810 |
Everest (Malaysia 1969) |
6377295,664 |
6356094,668 |
0,003324449297 |
300,801700000 |
0,0814729810 |
Everest (Malay, & Sing) |
6377304,063 |
6356103,039 |
0,003324449297 |
300,801700000 |
0,0814729810 |
Everest (Pakistan) |
6377309,613 |
6356108,571 |
0,003324449297 |
300,801700000 |
0,0814729810 |
Modified Fischer 1960 |
6378155,000 |
6356773,320 |
0,003352329869 |
298,300000000 |
0,0818133340 |
Helmert 1906 |
6378200,000 |
6356818,170 |
0,003352329869 |
298,300000000 |
0,0818133340 |
Hough 1960 |
6378270,000 |
6356794,343 |
0,003367003367 |
297,000000000 |
0,0819918900 |
Indonesian 1974 |
6378160,000 |
6356774,504 |
0,003352925595 |
298,247000000 |
0,0818205908 |
Hayford (International) 1924 |
6378388,000 |
6356911,946 |
0,003367003367 |
297,000000000 |
0,0819918900 |
Krassovsky 1940 |
6378245,000 |
6356863,019 |
0,003352329869 |
298,300000000 |
0,0818133340 |
GRS 80 |
6378137,000 |
6356752,314 |
0,003352810681 |
298,257222101 |
0,0818191910 |
South American 1969 |
6378160,000 |
6356774,719 |
0,003352891869 |
298,250000000 |
0,0818201800 |
WGS 72 |
6378135,000 |
6356750,520 |
0,003352779454 |
298,260000000 |
0,0818188107 |
WGS 84 |
6378137,000 |
6356752,314 |
0,003352810665 |
298,257223563 |
0,0818191908 |
Die Internationale Zivilluftfahrt Organisation (ICAO) hat 1998 das Referenzellipsoid WGS84 für die Ermittlung und Veröffentlichung von Positionsangaben in der Luftfahrt vorgeschrieben.
Allen nachfolgenden Berechnungen liegt das Referenzellipsoid von WGS84 zugrunde.
Die Einteilung der Erdoberfläche
Von der Kugelgestalt der Erde ausgehend, lag es nahe die zwei
senkrecht aufeinander stehenden Kreise in Winkel zu unterteilen. Also hat der Äquator
360° und der Kreis durch die Pole ebenfalls. Aber wo sollte man zu zählen beginnen?
Jedenfalls hat man sich irgendwann geeinigt.
Die Engländer setzten sich durch; sie definierten willkürlich den Längenkreis, der
durch ihre Sternwarte von Greenwich lief als 0°. Von hier aus gibt es demnach je 180° zu
beiden Seiten nach Osten und nach Westen. Der Längengrad 180° ist auch als Datumsgrenze
bekannt. Längengrade werden mit dem griechischen Buchstaben l (lambda) gekennzeichnet
Der Bezugsbreitengrad 0° wird vom Äquator physikalisch vorgegeben. Vom Äquator aus
wird nun zu beiden Seiten nach Norden und nach Süden jeweils 90° eingeteilt. Der
griechische Buchstabe für den geographischen Breitengrad ist j
(phi).
Breitenkreise |
|
Längenkreise |
|
Besonderheit des Breitenkreises
Der geographische Breitengrad j (phi) gibt an, um welchen Winkel der lokale Horizont eines Ortes gegen die Erdachse geneigt ist.
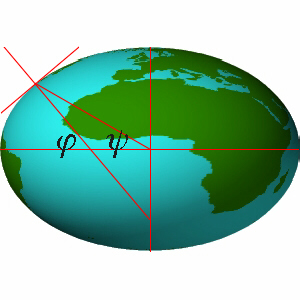
Der Horizont schmiegt sich als Tangente an die Oberfläche der
Ellipse. Der Zenit steht senkrecht über dem Horizont. Diese Linie schneidet aber nicht
den Erdmittelpunkt.
Eine Linie vom Erdmittelpunkt zum Schnittpunkt des Horizontes mit dem Zenit bildet zur
waagerechten Erdachse den Winkel y (psi), der als geozentrische
Breite bezeichnet wird. Der Winkel der geozentrischen Breite ist immer geringer als der
entsprechende geographische Breitengrad. Die geozentrische Breite errechnet sich nach
folgender Formel:
Zu den Polen und zum Äquator hin nähern sich geographische und geozentrische Breite an und erreichen als Differenz den Wert 0. Nachfolgendes Diagramm veranschaulicht dies und zeigt die größte Abweichung bei 45° geographischer Breite.
WGS84 Ellipsoid |
|
Kreis: U = Umfang, r = Radius |
Ellipse: U = Umfang, a = große
Halbachse, |
U = 2pr |
U ist der Grenzwert der Reihe für e < 1 |
| Äquator = 40075,0166855785 km | Längenkreis = 40007,8629172458 km |
Hier nur ein kurzer Hinweis für die Berechnung von Raumkörpern: Es
gibt unterschiedliche Bezeichnungen für die Oberflächen oder Teile der Oberfläche von
Raumkörpern. Bei der Abwicklung von Zylindern und Kegeln beinhaltet die Oberfläche O
jeweils auch die Fläche der/des Begrenzungskreis(es). Im Gegensatz zur Mantelfläche M,
die nur die Fläche der Abwicklung enthält.
Bei einer Kugelzone sind in der Mantelfläche M die beiden Flächen der jeweiligen
Begrenzungskreise nicht enthalten.
Ebenso ist es bei einem Rotationsellipsoid. Die Ellipsoidzonenfläche Z enthält nicht
die Fläche der beiden Begrenzungskreise.
Zylinder: M = Mantelfläche, h = Höhe, r = Kreisradius |
M = 2prh |
Kugelzone: M =(Mantel) Zonenfläche, h = Höhe, r = Kugelradius |
M = 2prh |
Rotationsellipsoid: Z = Zonenfläche, b = kleine Halbachse, a = große Halbachse, y = geozentrische Breite |
Die Vision von Arno Peters basiert, meiner Meinung nach, auf einem
besonders ausgeprägtem Gleichheitsgedanken und Wahrheitsgefühl.
Es ist wahr; geschichtliche Ereignisse haben zeitgleich an unterschiedlichen
geographischen Orten stattgefunden. Demnach hat jedes geschichtliche Ereignis das Recht
auf einen eigenen Platz auf einer gleichförmigen Zeitskala. Dies hat Arno Peters in
seiner "Synchronoptischen Weltgeschichte" eindrucksvoll visualisiert.
Alle Länder, die ein Staatsgebiet haben, besitzen auch eine geographische Fläche.
Wer wollte sich heutzutage anmaßen über die Wertigkeit von Ländern zu urteilen? Alle
Länder dieser Erde haben das gleiche Recht, auf einer Erdkarte gemäß ihrer Fläche
wirklichkeitsgetreu abgebildet zu werden. Diese gerechte Darstellung ist Arno Peters mit
der Konstruktion seiner Weltkarte gelungen.
Irgendwann hat man erkannt, dass man die Oberfläche einer Kugel
nicht abwickeln kann, um sie zweidimensional darstellen zu können. Also ersann man ein
Verfahren, die Oberfläche einer Kugel auf einen Raumkörper zu übertragen, der sich
geometrische abwickeln lässt. Das Zauberwort der Kartographie heißt
"Projektion".
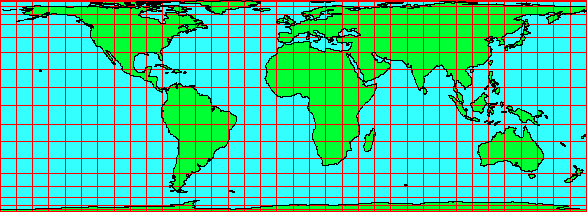
Es wird unterstellt, dass die Wasserflächen auf der Erdoberfläche durchsichtig sind. Nun
wird im Mittelpunkt der Erde eine Lampe angeknipst. Über die Erdkugel stülpt man einen
transparenten Raumkörper und schon braucht man nur die Umrisse der Schatten, die die
Landmassen werfen, nach zu zeichnen. Wickelt man nun den Raumkörper ab, erhält man die
Erdoberfläche auf einer zweidimensionalen Fläche. Einfach genial.
|
 |
|
|
Die Frage, die sich stellt ist: Lässt sich eine Landkarte ausschließlich durch eine Projektion erstellen? Die Antwort lautet: Nein ! Arno Peters hat ein System entwickelt, mit dem eine Landkarte durch rein mathematische Berechnungen erstellt werden kann. Deshalb wird die Art der Kartenerstellung von Arno Peters auch nicht als Projektion sondern als "Konstruktion" bezeichnet. Um die Peters-Konstruktion zu verstehen, muss man die Gedanken an eine irgendwie geartete Projektion der Erdoberfläche verdrängen und sich ganz dem mathematischen Aufbau zuwenden.
Nachfolgend wird das System erläutert, wie die Erdkarte gemäß der Peters-Konstruktion erstellt wird.
Begriffsdefinition |
||
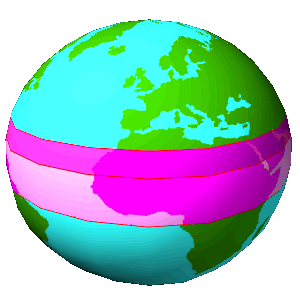 Ellipsoidzone |
 Zonenstreifen |
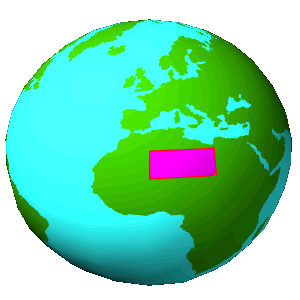 Zonensegment |
Ein Teil der Oberfläche eines Rotationsellipsoids zwischen dem Äquator und einem beliebigen Breitenkreis. |
Ein Teil der Oberfläche eines
Rotationsellipsoids zwischen zwei definierten Breitenkreisen. |
Ein definierter Anteil eines Zonenstreifens. |
Zur Verdeutlichung sind die Breitenkreise in 10° und die Längengrade in 20° Schritten eingezeichnet. |
||
Eine Netzmasche ist eine rechteckige Fläche aus denen sich ein Gitternetz zusammensetzt.
Ausgangsparameter für eine zu erstellende Erdkarte ist eine
waagerechte Strecke deren Länge von der gewünschten Breite der Erdkarte bestimmt wird.
Nehmen wir an, unsere Erdkarte soll 3,60 m (= 360 cm) breit werden. Diese Linie
repräsentiert den Äquator. Da es doppelt so viele Längen- wie Breitenkreise gibt, ist
demzufolge ein Zonensegment doppelt so breit wie hoch. Also ist das Zonensegment l = 2° breit und j = 1° hoch.
Die Grundlinie der Grundnetzmasche unserer Erdkarte ist demnach 360 cm / 180 = 2 cm
breit. Da die Grundnetzmasche ein Quadrat ist, beträgt auch die Höhe 2 cm.
Zuerst ermitteln wir die geozentrische Breite für geographischer Breite j = 1°und erhalten für y den Wert 0,993306966°. Dann setzten wir die bekannten Werte
in die Formel zur Berechnung von Ellipsoidzonen ein und erhalten 4431047,0014894 km².
Nunmehr wird diese Fläche durch 180 dividiert 4431047,001489400
/ 180 und wir erhalten den Flächeninhalt des Zonensegmentes von 24616,927786052 km².
Um die Seitenlänge eines Quadrates zu erhalten, ziehen wir die Quadratwurzel aus
dieser Fläche Ö24616,927786052 km² = 156,897825944 km. Diese Länge ist die
Basislinie und wird benötigt, um die Höhe aller nachfolgenden Netzmaschen zu errechnen.
Die Länge der Basislinie entspricht auf unserer Karte dem Verhältnis unserer Grundnetzmachenbreite
zur Basislinie 2 cm / 156,897825944 km = 0,012747149.
Durch die Umwandlung des Zonensegmentes in das Quadrat der Grundnetzmasche erfolgt eine Formverzerrung.
Mündungsdelta des Amazonas j = 0°N bis 1°N, l = 51°W bis 49°W |
|
Zonensegment |
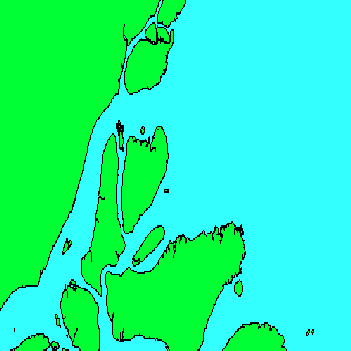 Grundnetzmasche |
Alle Netzmaschen in dem zu erstellenden Gitternetz haben eine gleiche Breite
(Grundlinie).
Alle Netzmaschen innerhalb eines Zonestreifens haben die gleiche Höhe.
Um die Höhe der nächsten Netzmaschenreihe zu errechnen wird für j = 2° der Wert y = 1,986622004°. Der
Flächeninhalt der Ellipsoidzone beträgt 8860780,38317385 km². Um den Flächeninhalt des
Zonenstreifens von j = 1° bis 2° zu erhalten, müssen wir von
der Fläche der Ellipsoidzone den Flächeninhalt der vorhergehenden Ellipsoidzone
subtrahieren = 8860780,38317385 km² - 4431047,0014894 km² = 4429733,38168445 km².
Der Flächeninhalt des Zonensegmentes = 4429733,38168445 / 180 = 24609,629898247 km². Die
Höhe dieses Zonensegmentes verhält sich wie der Flächeninhalt zur Basislinie
24609,629898247 km² / 156,897825944 km = 156,851312312 km.
Auf unserer Karte entspricht diese Höhe dem Wert 156,851312312 * 0,012747149 =
1,999407084 cm
Die Höhe einer Netzmasche verhält sich wie der Flächeninhalt des Zonensegmentes zur Basislinie.
Alle darüberliegenden Netzmaschen werden nach dem gleichen Schema berechnet.
| Erdoberfläche | Unsere Karte |
||||||
j |
y |
Ellipsoidzone | Zonenstreifen | Zonensegment | Höhe | Höhe | Teilhöhe |
| (°) | (°) | Z (km²) | Zx - Zx-1 (km²) | A = Zx / 180 (km²) | h (km) | h (cm) | hges (cm) |
1 |
0,993307 |
4431047,001489 |
4431047,001489 |
24616,927786 |
156,897826 |
2,000000 |
2,000000 |
... |
|||||||
10 |
9,934394 |
44093962,579799 |
4372034,074873 |
24289,078194 |
154,808252 |
1,973364 |
19,902277 |
20 |
19,876630 |
86881830,441838 |
4183281,499747 |
23240,452776 |
148,124760 |
1,888168 |
39,215034 |
30 |
29,833636 |
127088269,973908 |
3869280,153550 |
21496,000853 |
137,006365 |
1,746441 |
57,362637 |
40 |
39,810611 |
163500855,294729 |
3437827,233588 |
19099,040187 |
121,729158 |
1,551700 |
73,797843 |
50 |
49,810390 |
195004372,156136 |
2900248,357196 |
16112,490873 |
102,694163 |
1,309058 |
88,017289 |
60 |
59,833076 |
220616960,330178 |
2271530,040678 |
12619,611337 |
80,432034 |
1,025279 |
99,577802 |
70 |
69,875993 |
239526470,178184 |
1570231,881968 |
8723,510455 |
55,599945 |
0,708741 |
108,112809 |
80 |
79,933979 |
251124238,080918 |
818078,072684 |
4544,878182 |
28,967120 |
0,369248 |
113,347585 |
90 |
90,000000 |
255032810,842458 |
39192,005387 |
217,733363 |
1,387740 |
0,017690 |
115,111761 |
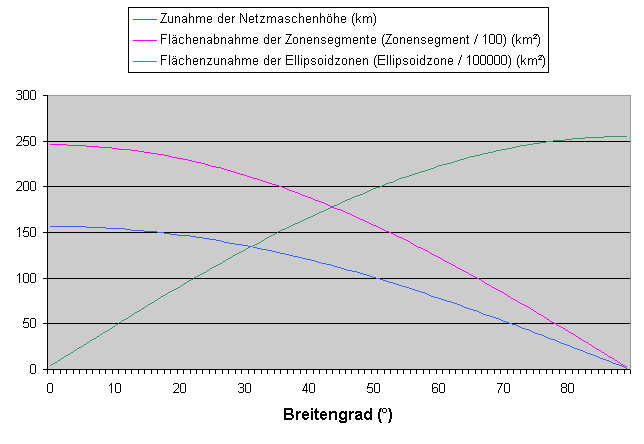
Dies ist nur ein Auszug aus der vollständigen Tabelle |
|||||||
 |
|||||||
Alle 16200 gewonnenen Netzmaschen (eingeschlossen sind auch die 180
Grundnetzmaschen) werden nun um den Äquator horizontal gespiegelt. Somit erhalten wir
auch das Gitternetz für die Südhalbkugel der Erde.
Anmerkung: Das Gitternetz muss gespiegelt werden, da der Wertebereich für die
Formel zu Berechnung der Ellipsoidzonenfläche nur von y = 0°
bis y = 90° gilt.
Für unsere Karte ergibt sich hges = 2 * hNord = 2 *
115,11176061 cm = 230,223521219 cm. Das Verhältnis Breite zur Höhe entspricht 360 cm /
230,223521219 cm = 1,563697741.
Für die Betrachtung der Genauigkeit sind zwei Aspekte unerlässlich. Zum einen der Kartennutzer, der erwartet, dass sich die Erdoberfläche so darstellt, wie es ihm seine verwendete Karte aufzeigt. Der Flieger vergleicht die vor ihm liegende Erdoberfläche mit dem Kartenbild und ermittelt so seine Position. Je nach Verwendungszweck variiert auch der Maßstab der verwendeten Karten. Demnach verwendet der Vermessungsingenieur, der das Grundstück eines Häuslebauers einmisst eine Karte mit größerem Maßstab als der Klimaforscher, der über die globale Erwärmung der Meere referiert.
Zum Anderen gibt es die Kartographen, deren Aufgabe darin besteht, Messdaten der Erdoberfläche auf eine zweidimensionale Karte zu übertragen. Für die Einzeichnung von Koordinaten bieten sich als Ausgangsmessbezüge definierte Linien an.
Da die Breite der Peters-Weltkarte willkürlich gewählt werden kann,
verhalten sich alle Längengrade linear zueinander. Die Bezugslinie für die Einzeichnung
von Längenkoordinaten ist also jeder beliebige Längengrad. Kein Problem.
Die Bezugslinie für die Einzeichnung von Breitenkoordinaten ist der Äquator. Die
Höhe der Netzmaschen nimmt zum Pol hin ab. Demnach verhalten sich auch die
Breitenkoordinaten innerhalb einer Netzmasche nicht linear.
Um eine beliebige Breitenkoordinate einzeichnen zu können, muss
zuerst das
Verhältnis des Flächeninhaltes der Ellipsoidzone, aus dem die Grundnetzmasche entwickelt
wurde, zur Basislänge bekannt sein. Flächeninhalt der Ellipsoidzone / Basislinie =
4431047,0014894 km² / 156,897825944 km = 28241,608669977 km.
Um z.B. die geographische Breite 30° einzuzeichnen, wird erst die geozentrische
Breite errechnet und anschließend der Flächeninhalt der Ellipsoidzone. Dann wird dieser
Flächeninhalt 127088269,973908 km² durch den Wert 28241,608669977 km dividiert =
4500,036504968 km.
Dieser Wert entspricht auf unserer Karte 4500,036504968 km * 0,012747149 =
57,362635834 cm.
Dieses Ergebnis lässt sich ebenfalls erzielen, indem man die Höhen aller 30
Netzmaschen berechnet und dann addiert. Allerdings treten mit dieser Methode spätestens
dann Probleme auf, wenn Dezimalbrüche (z.B. 37,839° nördlicher Breite) eingezeichnet
werden sollen. Für jedes 1/10 Grad Genauigkeit verzehnfacht sich die Anzahl der zu
berechnenden Netzmaschenhöhen.
Arno Peters hat gleichzeitig mit der Vorstellung seiner
mathematischen Kartenkonstruktion ein dezimales Längen- und Breitensystem für seine
Dezimalkarte eingeführt. Er verlegte willkürlich den Bezugslängengrad 0° zwischen die
Kontinente Russland und Amerika. Seine Länge 0° verläuft demnach fast ausschließlich
über Wasser. Dann zählt er 100 Längengrade nach rechts (Osten).
Seine Bezugslinie für die Breitengrade ist der geographische Nordpol. Von hier aus
zählt er 100 Breitengrade nach unten (bis zum Südpol). Für die Bestimmung einer
geographischen Koordinate würden also die Angaben nördliche oder südliche Breite bzw.
östliche oder westliche Länge entfallen.
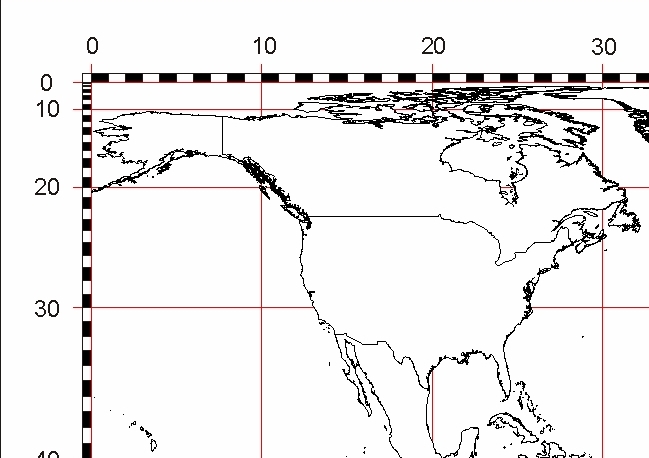
|
Nach der herkömmlichen Gradeinteilung verläuft der Längengrad 180° durch die Ostspitze von Russland. |
New York hat die geographischen Koordinaten 41° nördliche Breite 74° westliche Länge. |
Wollte man das dezimale Gradnetz für die Verwendung von Landkarten einführen, müssten weltweit alle erhobenen geographischen Messdaten auf das neue System umgerechnet werden. Ein aussichtsloses Unterfangen.
Das herkömmliche 360° Gradsystem basiert auf einer langen geschichtlichen Entwicklung durch die Beobachtung der Sonne und der Sterne. Dies hat unseren Kalender geprägt (365 Tage für einen Umlauf um die Sonne) sowie auch unser Zeitverständnis (24 Stunden für eine Eigendrehung der Erde). Sollte das Dezimalgradsystem eingeführt werden, müsste zwangsläufig unser Kalender und die Zeitdefinition angepasst werden. In der heutigen Zeit erscheint mir dies als unmöglich.
Arno Peters hat in seinem Atlas das alt bewährte 360° Gradnetz verwendet. Nur im hinteren Buchdeckel befindet sich seine Weltkarte mit dem Dezimalgradnetz. Auch auf seiner Erdkarte "Die Länder der Erde in flächentreuer Projektion" ist das herkömmliche Gradnetz aufgedruckt. Nur am Kartenrand ist die Einteilung gemäß seinem dezimalen System zu finden.
Bitte informieren Sie mich über alle fehlgeleiteten Verweise (Broken LINKS), vielen Dank.
Mit der Veröffentlichung dieser privaten Internetseite werden keinerlei
kommerzielle Absichten verfolgt.
Urheberrecht © Jürgen Heyn 2001, Alle Rechte vorbehalten
Datum der letzten Aktualisierung: 01. Dezember 2011