Select english language

Das Gall - Peters Missverständnis

von Jürgen Heyn

Im Gedenken an Prof. Dr. Arno Peters geboren am 22. Mai 1916 in Berlin gestorben am 2. Dezember 2002 in Bremen.

Aus persönlichem Interesse an der Peters-Karte durfte ich Prof. Dr. Peters in den vergangenen Jahren dreimal in seinem Haus in Bremen besuchen. Als ich ihn kennen lernte, war er ein freundlicher, älterer Herr mit wachen Augen und regem Geist.

Mich interessierte insbesondere: Wie funktioniert die Konstruktion der Peters-Karte und warum hat sie sich bis heute nicht allgemein durchgesetzt. Prof. Dr. Arno Peters hat alle meine Fragen bereitwillig und umfassend beantwortet. Es waren sehr informative und unterhaltsame Nachmittage; die Begegnung mit ihm hat in mir einen bleibenden Eindruck hinterlassen. Die Nachricht von seinem Tod hat mich sehr berührt. Mein Mitgefühl gilt seinen Angehörigen.
Wirklich tot ist nur jemand, an den sich niemand mehr erinnert. Prof. Dr. Arno Peters hinterlässt mit seiner "Peters-Karte" einen Teil seines Lebenswerkes, dessen sich noch Generationen nach ihm erinnern werden.

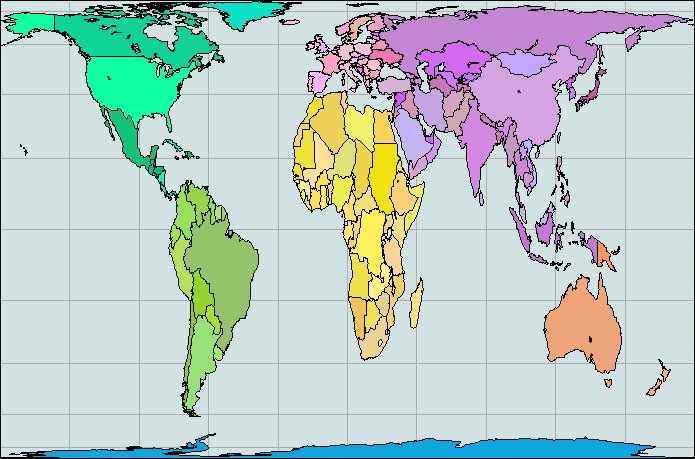
Das Konstruktionsprinzip der Peters-Karte habe ich bereits ausführlich beschrieben. Auf die Frage "Warum hat sie Peters-Karte nicht allgemein durchgesetzt"  erläuterte mir Prof. Dr. Arno Peters die Anfeindungen (Beispiel 1, Beispiel 2) gegen seine Person und gegen die von ihm entworfene Peters-Karte. Den Vorwurf der politischen Propaganda zu kommentieren sei Anderen vorbehalten. Aber den Vorwurf, er hätte die Idee für seine Karte von Rev. James Gall übernommen und Ruhm und Ehre für sich selbst beansprucht, möchte ich mit den nachfolgenden Ausführen widerlegen.

Bereits 1958 ist es Arno Peters in seiner "Synchronoptischen Weltgeschichte" gelungen die Gleichzeitigkeit geschichtlicher Ereignisse graphisch darzustellen. Er beabsichtigte dieses Werk mit Hilfe von Landkarten in Form eines Atlas zu veranschaulichen. Auch hier war ihm die Gleichwertigkeit äußerst wichtig.
Unter diesem Gesichtspunkt bewertete er die gebräuchlichsten Landkarten. Er verwarf die quadratische Plattkarte und die Mercator Projektion (Normalansicht), weil sie die Länder der Erde nicht gleichwertig (flächentreu) darstellen können.

Arno Peters verwarf ebenfalls alle Weltkarten mit gerundeten Längengraden. Obwohl es durchaus flächentreue Projektionen gibt, wird die Nord-Süd Ausrichtung zum Kartenrand hin in einem Maß verzerrt, die für ihn nicht akzeptabel war.
Durch umfangreiche Nachforschungen erkannte Arno Peters, dass die Rechtwinkligkeit einer Weltkarte den Menschen wichtiger war, als alle anderen Kartenqualitäten, wie zum Beispiel die Flächen- oder Winkeltreue.
Die ihm bekannten flächentreuen und rechtwinkligen Weltkarten waren die von Heinrich Lambert aus dem Jahre 1772 und die von Walter Behrmann, vorgestellt in Berlin 1910.

Aber auch diese Weltkarten erfüllte nicht die Anforderungen, die Arno Peters für seine Zwecke aufgestellt hatte. Mitteleuropa, Kanada und Russland sind in der Höhe zu stark zusammengedrückt.

Also versuchte Arno Peters eine eigene Karte zu entwickeln. Für ihn galt folgender Grundsatz: Für die Entwicklung einer flächentreuen Karte muss die Ausgangsgröße ein bekannter Flächeninhalt sein. Für seine ersten Versuche verwendete er die Bessel'sche Ellipsoidtabelle, in der die Flächeninhalte von je 1° Längen- und Breitengrad angegeben waren.
Als Nicht-Mathematiker ging er das Problem zeichnerisch an, indem er eine waagerechte Linie von 100 cm Länge zeichnete, die den Äquator repräsentierte.  Er entschloss sich sein Gitternetz im Dezimalsystem mit 100 * 100 Flächen zu entwickeln und zeichnete entlang seines Äquators 100 Quadrate mit je 3,6° (Umfang 360° / 100) Längendifferenz und 1,8° Breitendifferenz (1/2 Längenkreis 180° / 100) weil es doppelt so viele Längengrade wie Breitengrade gibt. Er legte seine vertikale Nulllinie (linker Kartenrand) in die Behringsee (168,6° W). Somit befindet sich das nordamerikanische Festland in der linken Kartenhälfte, während sich das gesamte asiatische Festland auf der rechten Hälfte befindet.

Für die Berechnung des Flächeninhaltes wandte er folgende Näherungsformel an:

Mit Hilfe dieser Formel errechnete Arno Peters 50 Flächeninhalte für die nördliche Erdhalbkugel.

Er ermittelte die Seitenlänge des ersten Quadrates, (welches auf dem Äquator liegt) indem er die Wurzel aus dem ersten Flächeninhalt zog. Er nannte diese Quadrat "Grundnetzmasche"; die Seitenlänge bezeichnet er als "Basislinie". Da seine Karte rechtwinklig werden sollte, mussten alle weiten Flächen die gleiche Breite (Basislinie) haben. Da die Flächeninhalte mit zunehmendem Breitengrad abnehmen, mussten auch die Höhen aller weiten Flächen abnehmen. Er erreichte dies, indem er jeden weiten Flächeninhalt durch die Basislinie dividierte. Um von der Höhe der Netzmaschen auf die Höhe der Rechtecke auf seiner Karte zu schließen, ermittelte er den Maßstabsfaktor (Breite der Grundnetzmasche seiner Karte dividiert durch die Basislinie (1 / 282,37 = 0,003541)). Durch einfache Grundrechenarten hat er die Höhe jedes weiteren Rechteckes gemäß seiner gewünschten Kartenbreite berechnet.

Die Planrechtecke für die südliche Erdhalbkugel gewann Arno Peters durch Spiegelung um den Äquator.

Peters Dezimal-Gitternetz

Für das Einzeichnen von geographischen Breitenkoordinaten errechnete Arno Peters den Flächeninhalt zwischen dem Äquator (0°) und dem gesuchten Breitengrad mit Hilfe der Näherungsformel. Das Ergebnis dividiert durch die Basislinie und anschließender Umrechnung auf den Kartenmaßstab ergibt die Kartenhöhe vom Äquator.

Peters Dezimal-Karte

Arno Peters war mit seiner Weltkarte zufrieden. Die Nord- (und Südländer) sind gut erkennbar. Die Formverzerrung hält sich in Grenzen. Selbst die Vertikale Verzerrung der äquatorialen Länder sind nicht so gravierend, als das sich die Länder nicht mehr  erkennen ließen.
In einem Vortrag am 6. Oktober 1967 vor  der Geographischen Klasse an der Ungarischen Akademie der Wissenschaften in Budapest stellt Arno Peters seine neu gewonnene Erdkarte vor und erläutert die geometrische Konstruktionsmethode.
Wenn die fachkundigen Zuhörer die Ähnlichkeit der Karte mit der des Rev. James Gall erkannt hätten, wäre Arno Peters bereits hier als Hochstapler entlarvt worden.

Von Zweifeln getrieben macht Arno Peters in den folgenden Jahren Versuche mit verschiedenen Zylinderprojektionen. Grundlage ist die Formel von Walter Behrmann (Standard Breitengrad bei 30° N/S):

x = Lambda * Cos(30°)    y = Sin(Phi) / Cos(30°)
(Anm.: Der Ausgangsraumkörper ist eine Kugel)

Zunächst projizierte er 5 Karten mit den Standard Breitengraden 35°, 40°, 45°, 50° und 55° N/S. Er gelangte zu der Überzeugung, dass die günstigste Projektion zwischen dem 40° und 50° liegen musste. Er projizierte 8 weitere Karten im Abstand von je 1° Breitengrad und kam zu dem Entschluss, dass die Projektion mit dem Standard Breitengrad von 45° die Günstigste sei.

Wäre Arno Peters zu dieser Zeit die Zylinderprojektion von Rev. James Gall bekannt gewesen, hätte er sich eine Menge Arbeit ersparen können. Wieso hätte er so umfangreiche und aufwendige Untersuchungen machen sollen, die bereits ein Anderer lange vor ihm gemacht hat? Zudem die Erkenntnisse die gleichen sind.

Seiner Erkenntnisse hat Arno Peters in einem Vortrag vor der Deutschen Gesellschaft für Kartographie in Berlin am 30. Oktober 1974 vorgestellt. In Bezug auf sein geometrisch gewonnenes Gradnetz führt er wörtlich aus:

Zitat: "Außerdem ist auch die Konstruktionsweise meiner Dezimalkarte noch einfacher als ihre Erstellung in Gestalt einer flächentreuen Schnittzylinderprojektion mit längentreuem Parallel auf dem 45. Breitenkreis. Dennoch habe ich keine Bedenken, wenn Sie aus praktischen Erwägungen - oder weil Ihnen diese Konstruktion vertraut ist - die letztere Arbeitsweise bei der Erstellung meiner Erdkarte vorziehen. Ihre Abweichung vom Original liegt innerhalb der Zeichengenauigkeit."

Wäre dem kompetenten Fachpublikum Gall's orthographische Projektion bekannt gewesen, hätte Arno Peters spätestens mit dieser Aussage Hohn und Spott geerntet. Dem aber war nicht so. Im Gegenteil, die Medien haben seine "neue" Erdkarte positiv gewürdigt.

Arno Peters war durchaus bewusst, dass auf seiner Weltkarte die Polarregionen unangemessen stark verzerrt sind. Deshalb schlug er für die Konstruktion von Einzelkarten folgendes Verfahren vor. Aus den jeweils begrenzenden Breitengraden wird das geometrische Mittel gebildet, das dann die neue Bezugslinie ist.

Es wäre sehr interessant zu erfahren, wann erstmals die verblüffende Ähnlichkeit der Peters-Karte und der Gall's orthographischen Projektion erkannt wurde. Mir scheint, dass sich die Kritiker nie wirklich mit der Konstruktionsmethode der Peters-Karte beschäftigt haben. Ansonsten kann ich mir kaum vorstellen, dass jemand die Konstruktionsmethode von Arno Peters nur für eine "Modifikation" bereits bekannter flächentreuer Zylinderprojektionen hält. Ob die Konstruktionsmethode von Arno Peters eine "revolutionäre Neuentwicklung" ist, sei dahingestellt. Mir ist jedenfalls keine Karte bekannt, die auch nur annähernd in ähnlicher Art einer geometrischen Konstruktion hergestellt wird.

Rev. James Gall aus Edinburg, Schottland hat in einem Artikel für "The Scottish Geographical Magazin" seine Projektionen bereits 1885 veröffentlicht. Die "Gall's Orthographic Projection" ist eine flächentreue Zylinderprojektion mit dem Standard-Breitengrad bei 45° N/S:

Flächentreue Zylinderprojektion (Standard-Breitengrad bei 45° N/S)
Animation	Animation

Zitat: "I have wondered why geographers never thought of using the Isographic projection with the latitudes rectified at the 45th parallel."
[Übersetzung: "I habe mich gewundert, warum die Geographen niemals über die Verwendung der isographischen Projektion mit dem Standard-Breitengrad von 45° nachgedacht haben."]

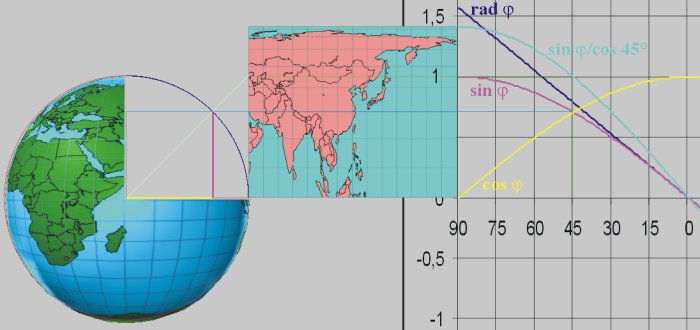
Der Winkel von 45° im Einheitskreis (r = 1) teilt ein Quadrat in 2 gleichseitige Dreiecke. Demzufolge sind der Sin(45°) = Cos(45°) und das Ergebnis der Division Sin(45°) / Cos(45°) = 1. Ein Rechteck bei 45° mit den Seitenlängen 2*1° Längengrad (2 * Cos(45°) ) und 1° Breitengrad (1 * Sin(45°)) hat den Flächeninhalt 1,414213 * 0,707106 = 1. Das gleiche Rechteck am Äquator hätte den Flächeninhalt 2 * 1 = 2. Die Quadratwurzel aus 2 = 1,414213. Dividiert man einen Flächeninhalt von 1 / 1,414213 = 0,707106781 (= Sin(45°) = Cos(45°)).

Die Erdkarten von Arno Peters und Rev. James Gall sind sich sehr ähnlich, aber sie sind nicht identisch. Eine Peters-Karte kann nur dann eine solche sein, wenn sie mit Hilfe des Konstruktionsprinzips von Arno Peters entworfen wurde. Jede andere Karte, die nicht gemäß diesem Konstruktionsprinzip entworfen wurde, kann demzufolge niemals eine Peters-Karte sein.

Wendet man die Formel für die flächentreue Zylinderprojektion einer Kugel x = Lamda * Cos(45°);  y = Sin(Phi) / Cos(45°) wird das Ergebnis niemals die Peters-Karte sein sondern die Gall's Orthographische Projektion. Wendet man das Konstruktionsprinzip von Arno Peters auf eine Kugel an, so wird das Ergebnis ebenfalls niemals eine Peters-Karte sein.

Um eine Karte mit den Abmessungen der Peters-Karte trigonometrisch projizieren zu können, muss die Formel für flächentreue Zylinderprojektionen auf einem Ellipsoid verwendet werden:

k = Cos(Phi₀) / Wurzel((1 - e^2 * Sin(Phi₀)^2))
q = (1 - e ^ 2) * (Sin(Phi) / (1 - e ^ 2 * Sin(Phi) ^ 2) - (1 / (2 * e)) * Log((1 - e * Sin(Phi)) / (1 + e * Sin(Phi))))
(Anm.: Log ist der natürliche Logarithmus zur Basis e = 2,718281...)
x = a * Lambda * k
y = a * q / (2 * k)

(siehe vollständige Tabelle)

Um eine Gall's Orthographische Erdkarte nach dem geometrischen Prinzip von Arno Peters zu konstruieren, müssen die Flächeninhalte für eine Kugeloberfläche (Mantelflächen) berechnet werden:

M = 2 * Pi * r * h

(siehe vollständige Tabelle)

Fazit: Prof. Dr. Arno Peters hat mir seine teils handschriftlichen Aufzeichnungen gegeben, die er damals gemacht hat. Unter anderem eine Liste mit Quellenhinweisen (Seite 1, Seite 2, Seite 3), die er aufmerksam studiert hat, als er sich erstmals mit den Themen Geographie und Kartographie beschäftigt hat. Des weiteren eine Anleitung (Seite 1, Seite 2) zum Erstellen einer Peters-Karte, die er für eine Schulklasse im April 1967 verfasst hat.

Ich habe die Quellen, soweit sie mir zugänglich und verfügbar waren, geprüft.
Nur in dem Buch: "Die Kartenwissenschaft" Band 1 [Forschungen und Grundlagen zu einer Kartographie als Wissenschaft] von Max Eckert, Berlin und Leipzig 1921 habe ich einen Hinweise auf Rev. James Gall gefunden:
Seite 116 Zitat: "Soweit mir die englische Kartenliteratur bekannt ist, habe ich bloß schwache Ansätze zum Betreten selbständiger Wege in die Projektionslehre gesehen, und zwar da, wo es sich um ältere Zylinderprojektionen oder um Modifikationen der Mercatorprojektion (Gall) handelte."
Seite 173 Zitat: "Bartholomew, der der Mercatorprojektion auch nicht kritiklos gegenüberstand, half sich im Challangerwerk und in anderen Publikationen dadurch, daß er eine Projektion anwandte, die als "Galls Stereographic Projection" bezeichnet wird."
Beide Aussagen bringen Rev. James Gall direkt in Verbindung mit der Mercatorprojektion, die Arno Peters bereits wegen der fehlenden Flächentreue verworfen hatte.

Ansonsten konnte ich nirgendwo einen Hinweis auf die flächentreue Zylinderprojektion von Rev. James Gall finden. Das stützt die Beteuerungen von Arno Peters, dass er die Idee nicht "gestohlen" hat.  Ich bin fest überzeugt, dass Arno Peters die "Gall's Orthographic Projection" nicht kannte, als er seine Konstruktionsmethode entwickelte. 

Arno Peters hat sich nie gegen die erhobenen Vorwürfe zur Wehr gesetzt. Möglicherweise haben seine Gegner dies als sogenanntes "Schuldeingeständnis" gewertet.

Die Behauptung, die "Gall's Orthographic Projection" und die Peters-Karte seien identisch, ist haltlos und unbegründet. Für die allgemeine Darstellung aller Länder dieser Erde auf einer Weltkarte bevorzuge und empfehle ich die "Peters-Karte".

Bitte informieren Sie mich über alle fehlgeleiteten Verweise (Broken LINKS), vielen Dank.